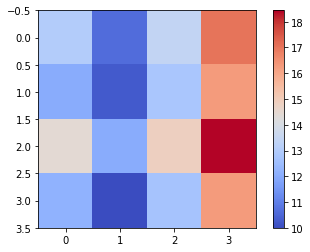MindNotes - Programming Basics - Python Introduction

Author: Christian M.M. Frey
E-Mail: christianmaxmike@gmail.com

Introduction to Python

In this tutorial, I want to give you a short hands-on introduction in Python and some insights in the basic usage of some common libraries in the scope of Data Science.

First steps

Assigning Values to Variables. Create variables and assign numbers, strings, floating values to them.

# assigning string to variables
animal = "koala"
person = "Homer"

# assigning integer to a variable
no_roi = 350

# assigning float value to a variable
avg_amount = 7.5 

# print to console
print (animal)

koala

Comments

#This is a comment
'''
This is a block comment
going
over
several 
lines
'''
print ("hello")  # another comment

hello

Variable types

In the following, let’s have a look at some basic variable types.
Python has five standard data types −

• Numbers
• String
• List
• Tuple
• Dictionary

Numbers.

We have already seen how to assign a value to a variable

solution = 42
answer = 1337.1337

Strings.

Strings are a sequence of characters.

my_team = "awesome Team!"

Lists.

Create a list which contains all numbers from 0 to 10

l0 = [1,2,3,4,5,6,7,8,9,10]
l0 = list(range(0,10))
l0

[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]

List Comprehensions.

Now, generate a list which contains all numbers from 0 to $n$ which have been squared using list comprehensions.

l3 = [x for x in [x**2 for x in range(7)] if x%2 !=0]
print(l3)

[1, 9, 25]

List reverse.

Given the following list $a=[0,1,2,3,4,5]$. Write a function which reverses the list.

a = [0,1,2,3,4,5]
a[::-1]

[5, 4, 3, 2, 1, 0]

Tuple.

A tuple is a collection of various variables contained in one container. In python, it is allowed that a tuple contains values of different types.

tuple_of_numbers = (4, 4.5, 0)  # integer, float value, integer
tuple_simpsons = ("Homer", 10.0, "Marge", 1, ['Bart', 'Lisa', 'Maggie']) # string, float value, string, integer, list

print (tuple_simpsons)

('Homer', 10.0, 'Marge', 1, ['Bart', 'Lisa', 'Maggie'])

Dictionaries I.

Create a dictionary with $n$ entries, where the keys are enumerated from $0$ to $n-1$ and the values are their corresponding keys squared. Use list comprehensions.
Example for expected result: $n = 7; {0:0, 1:1, 2:4, 3:9, 4:16, 5:25, 6:36}$

d1 = {x : x**2 for x in range(7)}
print(d1)

{0: 0, 1: 1, 2: 4, 3: 9, 4: 16, 5: 25, 6: 36}

Dictionaries II.

Use the dictionary from the previous assignment. Write a list comprehension to get a list of all the keys of the dictionary.

#it actually corresponds to d.keys()
dlis = [d1[x] for x in d1]
print(dlis)

[0, 1, 4, 9, 16, 25, 36]

Loops and conditionals.

Using the created list, print each element of the created list if its is an odd number, by using a loop and conditionals. Try using different type of loops.

# Version with for-loop
for e in l1:
    if e%2 != 0:
        print(e)

1
3
5
7
9

# Version w/ while-loop
i = 0
while i <len(l1):
    # if l1[i] %2 != 0:
    #     print(l1[i])
    if l1[i] & 1:
        print (l1[i])
    i+=1

1
3
5
7
9

#Version with list comprehension
l2 = [x for x in l1 if x%2 !=0]
print(l2)

[1, 3, 5, 7, 9]

Functions.

Write a function which takes an integer $n$. The function first creates a list of numbers from $0$ to $n$. Then, squares each number of the list. Further each of the squared numbers is tested if it is odd. All odd numbers are then appended to a new list. The function returns the list of odd (squared) numbers.

def get_odd(n):
    return [x for x in [x**2 for x in range(n)] if x%2 !=0]

print(get_odd(7))

[1, 9, 25]

Assignments (more in-depth)

Given a list $a=[‘I’,’like’,’cookies’]$ and another list $b=a$. Replace in the list $b$ the word $’cookies’$ with $’apples’$. Finally, print both lists ($a$ and $b$). What do you observe? What leads to the observed behavior?

a = ['I','like','cookies']
b = a

b[2] = 'apples'
print("list a: "+str(a))
print("list b: "+str(b))

print(id(a),id(b))

list a: ['I', 'like', 'apples']
list b: ['I', 'like', 'apples']
140232357655496 140232357655496

Shallow Copy I.

Given a list $a=[‘I’,’like’,’cookies’]$ and another list which takes a shallow copy of $a$, $b=a[:]$. Like in the previous assignment, replace in the list $b$ the word $’cookies’$ with $’apples’$. Finally, print both lists ($a$ and $b$). What do you observe now?

a3 =  ['I','like','cookies']
b3 = a3[:]
b3[2] = 'apples'
print("list a3: "+str(a3))
print("list b3: "+str(b3))
print(id(a3),id(b3))
print(id(a3[2]),id(b3[2]))

list a3: ['I', 'like', 'cookies']
list b3: ['I', 'like', 'apples']
140232357006472 140232357622152
140232357705968 140232357703952

Shallow Copy II.

Now, we are given a list $a = [‘I’, ‘like’, [‘chocolate’, ‘cookies’]]$. Another list $b = deepcopy(a)$ takes this time a deep copy from $a$. Change now the work $’cookies’$ with $’apples’$ in $b$. Print both lists ($a$ and $b$). What do you observe now?
Hint: For deep copy. first type: from copy import deepcopy

from copy import deepcopy

a4 =  ['I','like',['chocolate', 'cookies']]
b4 = deepcopy(a4)
b4[2][1] = 'apples'
print("list a4: "+str(a4))
print("list b4: "+str(b4))
print(id(a4[2]),id(b4[2]))

list a4: ['I', 'like', ['chocolate', 'cookies']]
list b4: ['I', 'like', ['chocolate', 'apples']]
140232357729224 140232356368584

Lambda functions.

Write a list comprehension which takes a number $n$ and returns a list with even numbers, using a lambda function.

even1 = lambda x: x%2 ==0
l7 = [x for x in range(7) if even1(x)]
print(l7)

[0, 2, 4, 6]

Python’s Builtin-Functions (excerpt)

map.

First, write a function which takes a length in $inch$ and returns a length in $cm$. Given a list $l$ with lengths in $inches$: $l=[4,4.5,5,5.5,6,7]$. Write a list comprehension which takes $l$ and returns a list with all values converted to $cm$ using $map()$.

linch = [4,4.5,5,5.5,6,7]

def inch_to_cm(length):
    return length*2.54

lcm = list(map(inch_to_cm, linch))
print(lcm)

filter.

Write a list comprehension which filters the list $l$ from the assignment above by returning only sizes between $4$ and $6$ $inches$.

lrange = list(filter(lambda x: x > 4 and x < 6, linch))
print(lrange)

reduce.

Write a list comprehension which reduces the list $l$ by summing up all lenghts.
Hint: for using the reduce function, you need to import it first by: from functools import reduce

from functools import reduce
lsum = reduce(lambda x,y: x+y, linch)
print(lsum)

Zipping of lists.

Given the following two lists, wher eone list represents the $x-Coordinate$ and another one the $y-Coordinate$:

• $xcoors = [0,1,2,3,4,5]$
• $ycoors = [6,7,8,9,10,11]$

Write a function which zips the two lists to a list of coordinate-tuples:

• $xycoors = [(0,6),(1,7),(2,8),(3,9),(4,10),(5,11)]$

xcoors = [0,1,2,3,4,5] 
ycoors = [6,7,8,9,10,11]
zcoors = [99, 98, 97, 96, 95, 94]

#'manual zipping'
def manualzip(lisa, lisb):
    reslis = []
    for i in range(min(len(lisa),len(lisb))):
        reslis.append((lisa[i],lisb[i]))
    return reslis

print(manualzip(xcoors,ycoors))

print(list(zip(xcoors,ycoors, zcoors)))

Unzipping of lists.

Now, we are given a list of data points where the first dimension of each data point represents the age of a person and the second dimension the amount of money spent for chocolate per month in euro:

• $chocage = [(20,8), (33,18), (27,14),(66,23),(90,100)]$

Write a function which takes the list and separates it into two lists, one containing the ages and another one containing its corresponding amount of money spent for chocolate. The result would be e.g.:

• $age = [20,33,27,66,90]$
• $money_spent = [8,18,14,23,100]$

chocage = [(20,8), (33,18), (27,14), (66,23), (90,100)]

#'manual unzipping'
def manualunzip(tuplelis):
    lisa = []
    lisb = []
    for e in tuplelis:
        a, b = e
        lisa.append(a)
        lisb.append(b)
    return [tuple(lisa),tuple(lisb)]

print(manualunzip(chocage))
    
print(list(zip(*chocage)))

Object oriented programming I

We deal now with object oriented programming in Python. For this purpose perform the following steps:

• Write a $Point$ class. A $Point$ class takes and $x$ and $y$ coordinate as an argument.
• Further this class shall have a setter method $setXY$ which takes and $x$ and $y$ coordinate and sets the attributes to the new provided values.
• The class shall also have a getter method $getXY$ which returns the current $x$ and $y$ coordiantes of the point.
• Write a method distance which takes another $point$ object and returns the euclidean distance between the provided point and the point itself. Hint: Take import math to use math.sqrt(value) in order to compute the square root.

import math

class Point(object):
    
    def __init__(self, x, y):
        #java: this.x = x;
        self.x = x
        self.y = y
        
    def setXY(self, x, y):
        self.x = x
        self.y = y
        
    def getXY(self):
        return (self.x,self.y)
    
    def distance(self, otherpoint):
        d = (self.x-otherpoint.x)**2 + (self.y-otherpoint.y)**2
        return math.sqrt(d)

Object oriented programming II

In a next step, the task is to create a class $Shape$. For this purpose perform the following steps:

• Create a class $Shape$ which takes a name and a color as parameters.
• Define a method $area$ which just returns $0.0$.
• Define a method $perimeter$ which just return $0.0$.

Now, create a class Rectangle which inherits from $Shape$ and in which you $implement$ the $area$ and $perimeter$ methods.

class Shape(object):
    
    def __init__(self, name, color):
        self.name = name
        self.color = color
        
    def area(self):
        return 0.0
    
    def perimeter(self):
        return 0.0
    

class Rectangle(Shape):
    def __init__(self, corner, width, height, color):
        #super(...) 'equivalent':
        Shape.__init__(self, "rectangle", color)
        self.corner = corner
        self.width = width
        self.height = height
    
    def perimeter(self):
        return self.width*2 + self.height*2
    
    def area(self):
        return self.width * self.height
    
r = Rectangle(Point(4,4),10,5,'pink')
print('Perimeter of rectangle r: ',r.perimeter())
print('Area of rectangle r: ', r.area())
    

Numpy I - some basic functions

In this block, you will become familiar with the numpy library and some of its basic functionality. Please also consider to consult the documentation https://docs.scipy.org/doc/numpy-dev/index.html if needed. Solve the following tasks:

• Create an numpy array of floats containing the numbers from $1$ to $4$.
• Create the following matrix as a numpy matrix: $M = [[1,2,3], [4,5,6]]$.
• Get the shape of the matrix $M$.
• Check if the value $2$ is in $M$.
• Given the array $a = np.array([0,1,2,3,4,5,6,7,8,9], float)$. Reshape it to an $5\times2$ matrix.
• Transpose the previously introduced matrix $M$.
• Flatten matrix $M$.
• Given the array $b = np.array ([0,1,2,3], float)$. Increase the dimensionality of $b$.
• Create and $3\times3$ identity matrix.

import numpy as np

# Create an np array with float as type
arr0 = np.array([1,2,3,4], float)
arr0

# Create a 2x3 matrix using np arrays
arr1 = np.array([[1,2,3],[4,5,6]], float)
arr1[0,0]

# Get shape of an array
arr1.shape

# Get type of an array
arr1.dtype

# Check if a particular value is in the array
[1,2,3] in arr1

# Reshape an array e.g. 1x10 to an 5x2 array
arr2 = np.array(range(10), float)
#print(arr2)
arr3 = arr2.reshape((5,2))
#print(arr3)

# Fill matrix with specific value
arr4 = np.array(range(10))
arr4.fill(42)
print(arr4)

# Transpose an array
arr5 = np.array([[1,2,3],[4,5,6]], float)
arr6 = arr5.transpose()
print(arr5)
print(arr6)

# Flatten an array
print(arr6.flatten())

# Increasing dimensionality of an array
arr7 = np.array([1,2,3],float)
print(arr7)
print(arr7[:,np.newaxis])

# Array of ones and zeros
print("array of ones and zeros")
print(np.ones((2,3),float))
print(np.zeros((2,3),float))

# Get an identity matrix
print(np.identity(3,float))

[42 42 42 42 42 42 42 42 42 42]
[[1. 2. 3.]
 [4. 5. 6.]]
[[1. 4.]
 [2. 5.]
 [3. 6.]]
[1. 4. 2. 5. 3. 6.]
[1. 2. 3.]
[[1.]
 [2.]
 [3.]]
array of ones and zeros
[[1. 1. 1.]
 [1. 1. 1.]]
[[0. 0. 0.]
 [0. 0. 0.]]
[[1. 0. 0.]
 [0. 1. 0.]
 [0. 0. 1.]]

Numpy II - linear algebra and statistics.

This assignemtn has its focus on numpy function of the linear algebra and statistics domain. Solve the following tasks using numpy:

• Given the following two numpy array: $a=np.array([1,2,3], float)$, $b=([4,5,6],float)$. Compute the dot product of $a$ and $b$
• Given the following matrix $M = [[1,2,0], [-1,2,1], [0,2,1]]$, compute the determinant of $M$ by using the $linalg$ package of the numpy library.
• Compute the eigenvalues and eigenvectors of $M$
• Compute the inverse of $M$
• Given the numpy array $c=np.array([1,4,3,8,3,2,3], float)$, compute the mean of $c$
• using $c$, compute the median.
• given the following matrix $C=[[1,1], [3,4]]$, compute the covariance of $C$.

# DOT PRODUCT
arr8 = np.array([1,2,3],float)
arr9 = np.array([4,5,6],float)
print("The dot product of {} and {} is: {}".format(arr8,arr9, np.dot(arr8,arr9)))

The dot product of [1. 2. 3.] and [4. 5. 6.] is: 32.0

# DETERMINANT
arr10 = np.array([[1,2,0],[-1,2,1],[0,2,1]],float)
print("Computation of the determinant: " , np.linalg.det(arr10))

# COMPUTE EIGENVALUES AND EIGENVECTORS
eigenvals, eigenvecs = np.linalg.eig(arr10)
print("Eigenvalues:" , eigenvals)
print("Eigenvectors:\n" ,eigenvecs)

# COMPUTE INVERSE
print("Inverse:\n", np.linalg.inv(arr10))

Computation of the determinant:  2.0
Eigenvalues: [2.         1.00000001 0.99999999]
Eigenvectors:
 [[ 6.66666667e-01 -7.07106784e-01  7.07106779e-01]
 [ 3.33333333e-01 -4.86907397e-09 -4.86907523e-09]
 [ 6.66666667e-01 -7.07106779e-01  7.07106784e-01]]
Inverse:
 [[ 0.  -1.   1. ]
 [ 0.5  0.5 -0.5]
 [-1.  -1.   2. ]]

# COMPUTE MEAN AND MEDIAN
arr11 = np.array([1,4,3,8,9,2,3],float)
print("mean: ",np.mean(arr11))
print("median: ",np.median(arr11))

# COMPUTE COVARIANCE
arr12 = np.array([[1,1],[3,4]],float)
print('cov: ',np.cov(arr12))

mean:  4.285714285714286
median:  3.0
cov:  [[0.  0. ]
 [0.  0.5]]

Matplotlib - Plotting figures in Python.

In this assignment we are finally going to become familiar with the plotting library of Python. For this we solve the following tasks below. Please consider to consult the documentation if needed: https://matplotlib.org/contents.html.

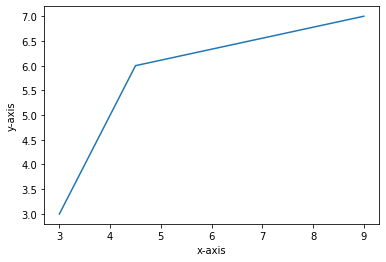
• Given a list of data points : $dpts=[(3,3),(4,5),(4.5,6),(9,7)]$. Plot the function using $plt.plot(xcoors, ycoors)$
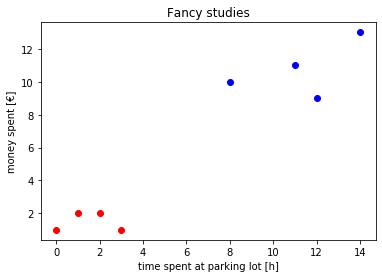
• You are given two tiny clusters $c_1 = [(1,2),(3,1),(0,1),(2,2)]$ and $c_2=[(12,9),(8,10),(11,11), (14,13)]$. Plot them in a scatter plot using $plt.scatter(xcoors, ycoors)$, where $c_1$ and $c_2$ have different colors. The $x-axis$ represents the time spent at a parking lot in hours, and the $y-axis$ represents the money spent in euro. Create axis labels for your figure.
• Take the two clusters $c_1$ and $c_2$ together and compute their pairwise distances, storing them in a matrix. Plot the resulting matrix as a heatmap using $plt.imshow(my_matrix, cmap=’coolwarm’)$.

import matplotlib.pyplot as plt
%matplotlib inline

#1 create data points and simple line plot
dpts = np.asarray([(3,3),(4,5),(4.5,6),(9,7)])
#access second column (y-coordinates)
print(dpts[:,1])

plt.figure()
plt.plot(dpts[:,0],dpts[:,1])
plt.ylabel('y-axis')
plt.xlabel('x-axis')
plt.show()


#2 scatter plot
c1 = np.array([(1,2),(3,1),(0,1),(2,2)])
c2 = np.array([(12,9),(8,10),(11,11),(14,13)])

plt.figure()
plt.scatter(c1[:,0],c1[:,1], color='r')
plt.scatter(c2[:,0],c2[:,1], color='b')
plt.xlabel('time spent at parking lot [h]')
plt.ylabel('money spent [€]')
plt.title("Fancy studies")
plt.show()


#3 More advanced: heatmap
from scipy.spatial import distance

distmx = []
for e in c1:
    newrow = []
    for f in c2:
        d = distance.euclidean(e,f)
        newrow.append(d)
    distmx.append(newrow)
    
for e in distmx:
    print(e)
    
plt.imshow(distmx, cmap='coolwarm', interpolation='nearest')
plt.colorbar()
plt.show()

[3. 5. 6. 7.]

[13.038404810405298, 10.63014581273465, 13.45362404707371, 17.029386365926403]
[12.041594578792296, 10.295630140987, 12.806248474865697, 16.278820596099706]
[14.422205101855956, 12.041594578792296, 14.866068747318506, 18.439088914585774]
[12.206555615733702, 10.0, 12.727922061357855, 16.278820596099706]

End of this MindNote