KMedoid
Published:

MindNote - Machine Learning - Unsupervised Learning - Clustering
Author: Christian M.M. Frey
E-Mail: christianmaxmike@gmail.com
K-Medoid
One potential problems of the K-Means algorithm is that an artificially defined centroid object might not make sense (e.g. if we think of categorial attributes). Another problem might be that there is only a distance function available but no explicit attribute-based data representation.
The KMeans algorithm is highly sensitive to outliers since an object with an extremely large value may substatntially distort the distribution of the data. Instead of taking the mean value of the objects in a cluster as a reference point, a Medoid can be used, which is the most centrally located object in a cluster. Hence, the partitioning can still be performed based on the principle of minimizing the sum of the dissimilarities between each object and its corresponding reference point (here: medoid - kmeans: geometrical centroid)
Partitioning Around Medoids (PAM):
The idea for the K-Medoid initialization is as follows:
- i) Select $k$ objects arbitrarily as initial medoids. These objects will be the representatives of the clusters (not as in k-means, where centroids are artifically created. These are no actual points in the dataset)
- ii) Assign each remaining (non-medoid) object to the cluster with the nearest representative
- iii) Compute the current total distance
Then the algorithm proceeds until a termination criteria is fullfilled. Let $\mathcal{M}$ be the set of Medoids and $X \setminus \mathcal{M}$ the set of non-Medoids. In the iterative process, we first identify for each pair $m \in \mathcal{M}$ and $n \in X \setminus \mathcal{M}$ (non-medoid) the total distance (= total cost) by swapping a medoid $m$ with a non-medoid $n$ object. We then choose the pair with the minimal cost and replace $m$ by $n$. If no further pair can be identified which will reduce our total costs, the algorithm terminates.
Load dependencies
%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns;
import numpy as np
sns.set()
from sklearn.metrics import silhouette_samples, silhouette_score
Generate dataset
from sklearn.datasets.samples_generator import make_blobs
X, y_true = make_blobs(n_samples=300, centers=4, cluster_std=0.60, random_state=0)
plt.scatter(X[:, 0], X[:, 1], s=50);
Implementation of KMedoid
import math
import matplotlib.cm as cm
class KMedoid (object):
"""
Implementation of the KMedoid algorithm
Arguments:
n_clusters: number of clusters
medoids: the medoids describing the cluster representatives
seed: random seed
Properties:
n_clusters: number of clusters
centroids: centroids being the cluster representatives
random_gen: random number generator (for initializing the centroids)
cls_labels: the labels of the datapoints,i.e., indicator to which cluster a point
is affiliated
"""
def __init__(self, n_clusters, medoids=None, seed=42):
self.n_clusters = n_clusters
self.medoids = medoids
self.random_gen = np.random.RandomState(seed)
self.cls_labels = None
def _total_cost(self, X, m_idx):
meds = X[m_idx, :]
distances = np.array([np.min([self._euclidean(x, m) for m in meds]) for x in X])
labels = np.array([np.argmin([self._euclidean(x, m) for m in meds]) for x in X])
return np.sum(distances), labels
def _euclidean (self, x, y):
"""
calculates the l2 distance between two vectors
Returns:
the l2 distance (euclidean distance)
"""
return math.sqrt(sum([(a - b) ** 2 for a, b in zip(x, y)]))
def _pick_random_medoids(self, X):
"""
method for initializing random medoids. Picks n random points out of the dataset,
where n is the number of clusters
Returns:
n number of centroids, where n is the number of clusters
"""
self.medoids_idx = self.random_gen.choice(X.shape[0], self.n_clusters, replace=False)
return X[self.medoids_idx, :]
def _plot_clustering(self, X, it):
"""
Method for plotting the current clustering. We plot the dataset, the current
medoids and colors indicate the cluster affiliation
Arguments:
X: the dataset the algorithm is performed on
it: the current iteration number
(can be used e.g. as an additional information in the title)
"""
plt.figure()
plt.title("Iteration {d}".format(d=it))
plt.scatter(X[:, 0], X[:, 1], c=self.cls_labels, s=50, cmap='viridis');
plt.scatter(self.medoids[:, 0], self.medoids[:, 1], s=100, c='w', edgecolor="red")
plt.title("The visualization of the clustered data.")
plt.xlabel("Feature space for the 1st feature")
plt.ylabel("Feature space for the 2nd feature")
def fit(self, X, max_iteration=100):
"""
Method used for executing the KMedoid algorithm.
Arguments:
X: the dataset
max_iteration: the maximal number of iterations being performed
"""
self.medoids = self._pick_random_medoids(X)
cost, labels = self._total_cost(X, self.medoids_idx)
self.cls_labels = labels
best_ = self.medoids_idx
c_cost = cost
it = 1
while True:
for i in range(0, len(self.medoids_idx)):
items_idx = np.where(self.cls_labels==i)
for item_idx in items_idx[0]:
medoids_idx_test = self.medoids_idx.copy()
medoids_idx_test[i] = item_idx
tmp_cost, c_labels = self._total_cost(X, medoids_idx_test)
if tmp_cost < c_cost:
best = medoids_idx_test
c_cost = tmp_cost
best_labels = c_labels
self._plot_clustering(X, it)
if np.all(best == self.medoids_idx):
break
if c_cost < cost:
cost = c_cost
self.medoids_idx = best
self.medoids = X[self.medoids_idx,:]
self.cls_labels= best_labels
it += 1
Run it!
kmedoid = KMedoid(n_clusters=4)
kmedoid.fit(X)
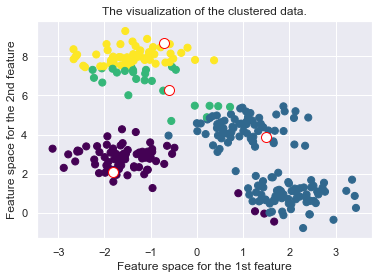
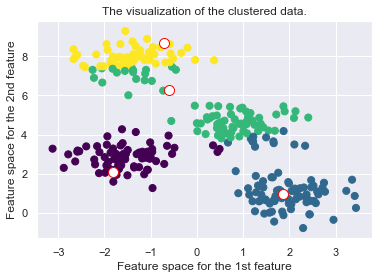
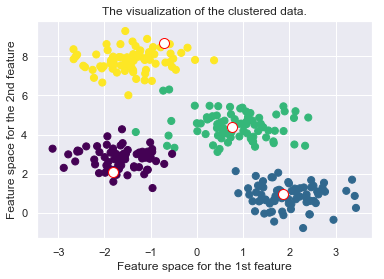
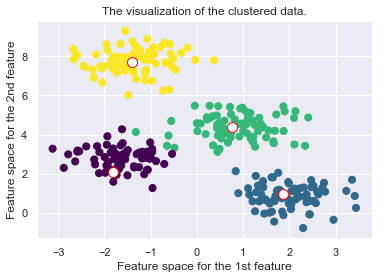
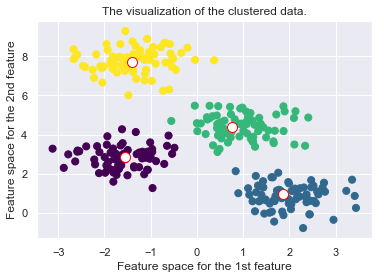
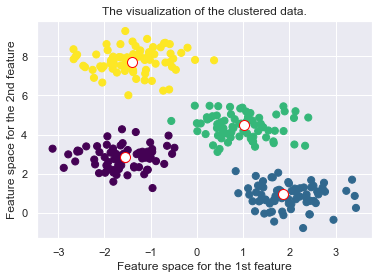
Drawbacks of the K-Medoid Algorithm:
- High complexity of each iteration O(k(n-k)^2). We have to find the distance between each of the (n-k) data points $k$ times to place the data points in their closest cluster. After that, we need to swap each of the previously assumed medoids with each non-medoids and recompute the distance between (n-k) objects. Hence, k-Medoids is more costly than the k-Means method
- Not suitable for clustering non-spherical groups of objects.
- the hyperparameter $k$ has to be set beforehand, i.e., the algorithm cannot identify the number of clusters by itself
- may obtain different results for different runs on the same dataset because the first $k$ medoids are chosen randomly
